Đóng góp của Đại sư Nhất Hạnh trong lĩnh vực thiên văn và toán học

Đại sư Nhất Hạnh là một nhân vật vĩ đại trong lĩnh vực thiên văn học cũng như Phật giáo, đặc biệt là Kim Cương thừa. Ngài đã đóng góp vào sự phát triển của thiên văn học lý thuyết, thiên văn học quan sát và toán học, cũng như lịch Dayan (大衍暦) là kết quả từ nghiên cứu thiên văn học của ngài.

Tác giả: Thích Nguyên Định

Lời dẫn

Đại sư Nhất Hạnh là một vị Tăng sĩ Phật giáo và nhà thiên văn học  (astronomer) trong triều đại nhà Đường (唐) của Trung Quốc. Mọi người đều biết rằng, ngài đã tạo ra một cuốn lịch xuất sắc mang tên Dayan-li (大衍暦) vào năm 727 STL, loại lịch này cũng từng được sử dụng ở Nhật Bản.

Trong bài viết này, chúng tôi muốn trình bày về đóng góp của đại sư Nhất Hạnh trong lĩnh vực thiên văn học và toán học. Dù sao đi nữa, trong lĩnh vực toán học, phương pháp nội suy của đại sư có thể được hiểu là sự phát triển tự nhiên của phương pháp nội suy của Trung Quốc vào thời nhà Tùy  (581-618 STL) và Đường (618-907 STL).

I. Đóng góp về thiên văn học của đại sư Nhất Hạnh

1. Đại sư Nhất Hạnh về lĩnh vực thiên văn học

Đại Sư Nhất Hạnh (C. 一行; J. Inchigyo, 683-727 STL) là đệ tử của ngài Thiện Vô Úy (S. Śubhākārasiṃha, 637-735). Nhất Hạnh là pháp danh của ngài, và thế danh là Trương Toại (張遂). Đôi khi còn gọi ngài với danh hiệu là Tăng Nhất Hạnh (僧一行) hoặc Nhất Hạnh thiền sư (一 行禪師). Ngài Nhất Hạnh nhận được lời mời từ Hoàng đế Huyền Tông (玄宗, 685-762 STL) vào năm 717 STL chuyển đến Trường An (長安) (ngày nay là Tây An, 西安), thủ đô lúc bấy giờ của Trung Quốc.

Sau đó, ngài Nhất Hạnh học Mật tông với các Đại sư Ấn Độ như Thiện Vô Úy (S. Śubhākārasiṃha, 637-735 STL) và Kim Cương Trí (S. Vajrabodhi, 671-741 STL) và đồng dịch kinh Đại Nhật (Mahāvairocana-tantra) (7 quyển), Tô Bà Hô Đồng Tử kinh (蘇婆呼童子請問經),[1] Tô Tất Địa Yết La kinh (蘇悉地羯羅經; Susiddhikara-mahātantra-sādhanopāyika-paṭala)[2] (3 quyển), Kim Cương Đảnh Du Già Trung Lược Xuất Niệm Tụng Kinh (金剛頂瑜伽中略出念誦經)[3] (4 quyển)…

Hơn nữa, ngài còn soạn thuật Đại Nhật Kinh Sớ (大日經疏)[4] (20 quyển), tích hợp tất cả các khía cạnh của Phật giáo Mật tông vào “pháp giới duyên khởi”; Phật giáo Mật tông cũng tiếp nhận pháp giới bổn tịnh, bao trùm vạn vật. Vì thế, dù trên mọi phương diện nào cũng không rời Trung đạo, tất cả các pháp đều là giáo lý của Phật giáo. Đại Nhật Kinh Sớ phát triển tư tưởng Bát nhã và phát huy tinh thần Bồ-tát hạnh.

Từ động cơ tiện lợi và vị tha, kết hợp với môi trường thực tế ở Ấn Độ lúc bấy giờ, đã hình thành một tông phái Đại thừa khác với Phật giáo nguyên thủy.

Vào năm 721 STL, theo yêu cầu của Hoàng đế, ngài nhất hạnh bắt đầu dự án làm một cuốn lịch mới. Ngài Nhất Hạnh và quan chức chính phủ tên là Lương Linh Toản (梁令瓚, 690-757 STL) đã tạo ra một hỗn thiên cầu (渾天球) vào khoảng năm 724 STL và quan sát các ngôi sao. Từ năm 724 STL, đại sư Nhất Hạnh đã tiến hành quan sát thiên văn tại một số nơi trên khắp Trung Quốc cùng với đồng nghiệp của mình là Nam Cung Thuyết (南宮說, ?).

Vào năm 725 STL, ngài Nhất Hạnh đã cùng Đề Lương (提 梁) tạo ra một quả cầu thiên thể điều khiển bằng nước. Sau những sự chuẩn bị này, ngài Nhất Hạnh bắt đầu biên soạn một lịch mới và hoàn thành bản thảo của Dayan-li (大衍暦, Đại diễn lịch) vào năm 727 STL, điều đáng tiếc là ngài viên tịch vào cuối năm đó. Tiếp tục sứ mạng có Trương Thuyết (張說, 667-730 STL) và Trần Huyền Cảnh (陳玄景)  biên tập bản thảo của ngài Nhất Hạnh và lịch Đại Diễn được chính thức sử dụng từ năm 729 STL.

Vào thời Tùy (隋, 581-618 STL) và Đường (唐, 618-907 STL), một số loại lịch tốt đã được tạo ra. Sau đây là lịch sử sơ bộ về lịch trước thời kỳ của ngài Nhất Hạnh. Lịch Hoàng Cực (皇極暦, 600 STL) của Lưu Trác (劉焯, 544-610 STL) không được sử dụng chính thức, nhưng là một loại lịch xuất sắc trong đó các bất đẳng thức (inequality) tương ứng với phương trình tâm mặt trời, mặt trăng và tuế sai (precession)[5] hay tiến động của các điểm phân đã được xem xét, đồng thời phép nội suy bậc hai cũng được sử dụng lần đầu tiên ở Trung Quốc.

Lịch Lân Đức (麟徳暦, 665 STL) của Lý Thuần Phong (李淳風, 602-670 STL) cũng là một loại lịch nổi tiếng, được sử dụng ở Hàn Quốc và Nhật Bản. Lý Thuần Phong không chỉ có những đóng góp đáng kể cho nghiên cứu thiên văn học và toán học mà còn có những kết quả nghiên cứu sáng tạo về khí tượng học.

Trên cơ sở tổng hợp kinh nghiệm trước đây, ông tiến hành quan sát, nghiên cứu sâu hơn về hướng gió và lực gió, đồng thời xác định được 24 loại hướng gió và 8 cấp độ gió. Ông là người đầu tiên trên thế giới thiết lập mức gió.

Hơn một nghìn năm sau, vào đầu thế kỷ XIX, người Anh đánh giá năng lượng gió ở mức 12. Lý Thuần Phong đã giới thiệu hai loại dụng cụ đo thời tiết trong cuốn sách “Ất Tỵ Chiêm” (乙巳占)[6] của mình, đây là chuyên luận khí tượng sớm nhất trên thế giới. Các tác phẩm khác của ông bao gồm “Điển chương văn vật chí” (典章文物志), “Diễn tề nhân yếu thuật” (演齊人要术), “Bí các lục” (秘閣录) v.v... tất cả đều đã bị thất lạc.

Sau đó, đại sư Nhất Hạnh đã soạn lịch Dayan (大衍暦), đây được coi là một trong những cuốn lịch hay nhất của nhà Đường. Sau thời ngài Nhất Hạnh có lịch Tuyên Minh (宣明暦,  822 STL) của Từ Ngang (徐昂, ?) cũng nổi tiếng và phương pháp dự đoán nhật thực cũng được cải tiến. Ngoài ra, lịch Sùng Huyền (崇玄暦, 892 STL) của Biên Cương (邊岡, 893-956 STL) cũng có một số thiết bị. Lịch Dayan (大衍暦) và lịch Tuyên Minh (宣明暦) được sử dụng ở Nhật Bản,  trong khi lịch Tuyên Minh cũng được sử dụng ở Hàn Quốc.

Triều đại nhà Đường cũng là thời kỳ thiên văn học Ấn Độ du nhập vào Trung Quốc. Theo Ôhashi, Yukio (大橋由紀夫, 1955-2019)[7] nhận xét: Một số thông tin về thiên văn học Ấn Độ có thể đã đến Trung Quốc vào thời Đông Hán (東漢, 25-220 STL).

Sau đó, một văn bản Phật giáo chứa đựng kiến thức về chiêm tinh và thiên văn học Ấn Độ, trong Divyāvadāna[8] có đề cập đến câu chuyện về Śārdūlakarṇa (S. Śārdūlakarṇa-avadāna; T. Stag-rna'i-rtogs-pa-brjod-pa, སྟག་རྣའི་རྟོགས་པ་བརྗོད་པ།),[9] đã được dịch sang tiếng Trung Quốc thời kỳ “Tam Quốc” (三国, 222-280 STL).

Vào thời nhà Đường, một tác phẩm chi tiết về toán học thiên văn Ấn Độ, lịch Cửu Chấp (九執暦, 718 STL),[10] được soạn bằng tiếng Trung Quốc bởi một nhà thiên văn học người Ấn Độ tên là Cù-đàm-tất-đạt (瞿曇悉達) tiếng Phạn gọi là Gotama-siddha, sử dụng làm tài liệu tham khảo trong cuộc tranh luận sôi nổi về cải cách lịch dưới triều đại Huyền Tông, và được đưa vào “Đại Đường Khai Nguyên Chiêm Kinh” (大唐開元占經) của ông. Cù-đàm-tất-đạt đã cư trú ở Trung Quốc từ thời ông nội.

Đại sư Nhất Hạnh cũng có một số kiến thức về thiên văn học Ấn Độ, nhưng lịch Dayan của ngài lại theo phong cách truyền thống của Trung Quốc. Sự thật này không thể không quên.

Vào thế kỷ thứ VIII STL, một phiên bản Trung Quốc của chiêm tinh học Ấn Độ, được sáng tác bằng tiếng Trung Quốc bởi một nhà sư Ấn Độ: Bất không kim cương (S. Amoghavajra, 705-774 STL)… Bất không kim cương là đệ tử của Kim cương trí (S. Vajrabodhi, 671-741STL), người mà Đại sư Nhất Hạnh đã cùng tham học.

2. Thiên văn học quan sát

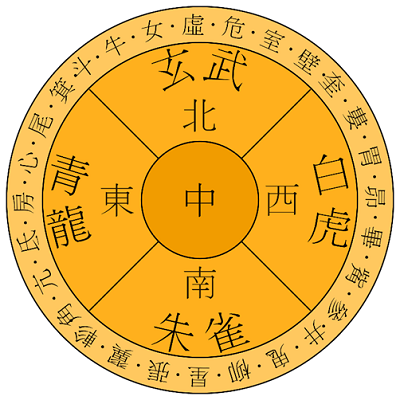
Đại sư Nhất Hạnh và Lương Linh Toản (梁令瓉) đã tạo ra một hỗn thiên cầu được gọi là “Hoành đạo du nghi” (黄道游儀) là một dụng cụ có vòng tròn hoàng đạo có thể di chuyển;  vào khoảng năm 724 STL (hình 1). Đúng như tên gọi, trên dụng cụ này, vòng tròn hoàng đạo có thể di chuyển theo tuế sai của các điểm phân.

Nó cũng có một vòng tròn di chuyển được cho quỹ đạo mặt trăng. Với thiết bị này, ngài Nhất Hạnh đã quan sát các ngôi sao, đặc biệt là trong 28 ngôi sao trên mặt trăng (二十八宿) (hình 2) và so sánh chúng với những quan sát trước đó, đo lường sự thay đổi về khoảng cách cực và độ thăng thiên bên phải của chúng. Những thay đổi này là do sự tuế sai của các điểm phân.

Ngài Nhất Hạnh và Lương Linh Toản cũng đã tạo ra một quả cầu thiên cầu chạy bằng nước vào năm 725 STL. Ngoài thiên cầu còn có hai tượng gỗ tự động đánh trống và chiêng (hình 3).

Từ năm 724 đến 725 STL, ngài Nhất Hạnh và Nam Cung Thuyết (南宮說) đã tiến hành quan sát thiên văn tại 13 địa điểm khác nhau trong khoảng từ khoảng 51° Bắc đến khoảng 18° Bắc. Họ quan sát độ cao của Cực Bắc, chiều dài của bóng đồng hồ mặt trời (gnomon) tại các điểm chí và các điểm phân, cũng như độ dài của ngày và đêm trong các điểm chí.

3. Thiên văn học lý thuyết

Lịch Dayan (大衍暦) của Đại sư Nhất Hạnh là một trong những cuốn lịch tốt nhất ở Trung Quốc và có một số tính năng quan trọng.

Ở Trung Quốc, bất đẳng thức tương ứng với phương trình tâm mặt trời được Trương Tử Tín (張子信, ?) phát hiện vào thế kỷ thứ VI STL, độc lập với sự khám phá của Hipparchus (190-120 Tr.TL)[11] ở Hy Lạp cổ đại. Theo sự bất đẳng thức này, ngài Nhất Hạnh đưa ra giá trị của 24 điểm thời gian trong một năm, được chia theo chuyển động góc của mặt trời. Ở đây, ngài Nhất Hạnh lần đầu tiên sử dụng phép nội suy bậc hai với các bước lập luận không bằng nhau ở Trung Quốc.

Đối với bất đẳng thức tương ứng với phương trình tâm mặt trăng, được phát hiện vào thế kỷ thứ nhất STL - thời Hậu Hán ở Trung Quốc, đại sư Nhất Hạnh đã sử dụng phép nội suy bậc hai với các bước lập luận bằng nhau do Lưu Trác (劉焯) phát minh ra vào năm 608 STL, đời nhà Tùy.

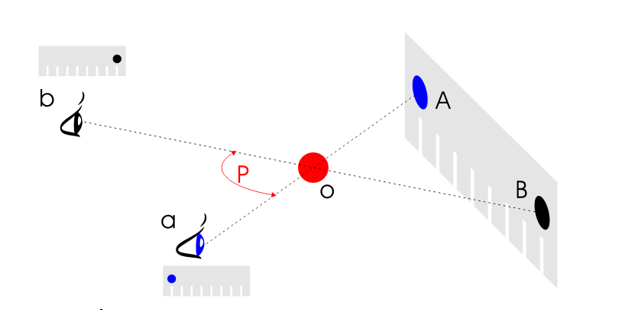
Với sự nỗ lực dự đoán nguyệt thực đã được bắt đầu bởi lịch Tam Thống (三統暦) của Lưu Hâm (劉歆, 50 Tr.Tl - 23 STL) vào cuối thời nhà Hán, và là cơ sở của hệ thống tiêu chuẩn dự đoán về nguyệt thực. Nhật thực và nguyệt thực được thiết lập theo lịch Kinh Sơ (景初暦, 237 STL) của Dương Vĩ (楊偉)[12] vào thời Tam Quốc. Để dự đoán nhật thực, ngài Nhất Hạnh đã xem xét thị sai[13] của mặt trăng ở những nơi khác nhau (hình 4).

Mặc dù phương pháp của đại sư không hoàn hảo nhưng đó là một bước tiến lớn. Phương pháp dự đoán nhật thực sau đó đã được Từ Ngang (徐昂) phát triển thêm trong lịch Tuyên Minh (宣明暦, 822 STL).

Ngài Nhất Hạnh cũng cải tiến cách tính toán vị trí của năm hành tinh và sử dụng một kiểu nội suy trong đó sử dụng sai phân thứ ba, mặc dù đó không phải là phép nội suy bậc ba.

Một trong những đóng góp khác của đại sư Nhất Hạnh là thiết bị tính toán độ dài của bóng đồng hồ mặt trời (gnomon) và độ dài của ngày và đêm ở các mùa khác nhau, cũng như ở những nơi khác nhau. Với mục đích này, đại sư đã lập một bảng bóng “gnomon” cho mỗi “độ Trung Quốc”,[14] từ 0 đến 81, khoảng cách thiên đỉnh (cực điểm, điểm cao nhất) của mặt trời. Bảng này là bảng tiếp tuyến sớm nhất trên thế giới.[15]

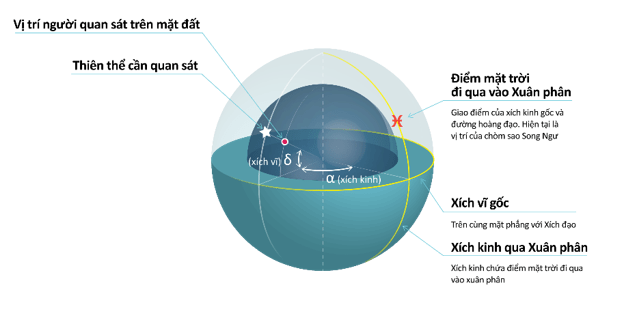
Để chuyển đổi tọa độ cầu, phương pháp đồ họa trên thiên cầu đã được sử dụng từ thời Hậu Hán. Một phương pháp số học đã được bắt đầu trong lịch Hoàng Cực (皇極暦), 600 STL) bởi Lưu Trác (劉焯), và ngài nhất hạnh cũng sử dụng phương pháp số học. Trong phương pháp này, sự khác biệt giữa xích kinh[16] bên phải và kinh độ cực (kinh độ của vòng tròn giờ cần thiết trên mặt phẳng hoàng đạo) (hình 5) được giả định là một hàm tuyến tính trong một góc phần tư và sự khác biệt được đưa ra trong một bảng.

Lịch Dayan (大衍暦) của ngài Nhất Hạnh được du nhập vào Nhật Bản và được sử dụng chính thức ở đó từ năm 746 đến năm 857 STL.

 4. Đại sư Nhất Hạnh và thiên văn học Ấn-độ

Ngài Nhất Hạnh có một số kiến thức về thiên văn học Ấn-độ. Ví dụ, ngài  đã đề cập đến cung hoàng đạo Ấn-độ trong lịch Dayan (大衍暦) của mình, nhưng ngài đã làm lịch Dayan theo cách truyền thống của Trung Quốc. Tuy nhiên, có một vài hoài nghi bởi ảnh hưởng của Ấn-độ trong lịch của đại sư Nhất Hạnh, và đây là sự thay đổi ý nghĩa của “mieri” diệt nhật (滅日).[17]

Đầu tiên chúng ta hãy xem ý nghĩa của từ này trước khi ngài Nhất Hạnh sử dụng nó. Lịch Hậu Hán Tứ Phần (後漢四分 暦, 85 STL) có những ngày đặc biệt gọi là “mori” (沒日, một nhật) và “mieri”, những ngày này không tồn tại vào thời Tiền Hán. Nếu một năm được chia thành 360 phần và một ngày được gộp vào một phần thì ngày đó được gọi là “mori”.

Nếu phần cuối của một ngày trùng với ranh giới của các phần thì ngày đó được gọi là “mieri”. Những ngày này không được sử dụng trong lịch truyền thống của Trung Quốc mà tương tự như một số khái niệm nhất định trong lịch truyền thống của Ấn Độ, chẳng hạn như phương pháp xen kẽ trong Artha-śāstra.[18]

Bây giờ, ngài Nhất Hạnh đã thay đổi ý nghĩa của “mieri”, giải thích phương pháp tính toán như sau: Hãy chia một tháng đồng bộ thành 30 phần. Sau đó, đôi khi một phần được đưa vào trong vòng một ngày. Ngày này chính là “mieri” được ngài Nhất Hạnh định nghĩa.

"Mieri" này của đại sư Nhất Hạnh tương tự như “tithi”[19] đã bị lược bỏ trong lịch Ấn-độ (Hindu). Trong thiên văn học Vedāṅga,[20] “tithi” là phần 1/30 của một tháng giao hội, trong đó phương trình tâm không được biết đến. Trong Thiên văn học cổ điển Ấn-độ giáo, “tithi” là khoảng thời gian trong đó sự khác biệt theo chiều dọc của mặt trời và mặt trăng thay đổi 12°. Nếu một “tithi” được đưa vào trong một ngày thì “tithi” được gọi là “tithi bị bỏ qua.”

Trong lịch truyền thống của đạo Hindu, tên của một ngày dân sự được xác định bởi số “tithi” vào lúc bắt đầu (mặt trời mọc) trong ngày. Do đó, con số “tithi bị bỏ qua”, không bao gồm mặt trời mọc, thực sự biến mất khỏi lịch.

Ý nghĩa trong định nghĩa của ngài Nhất Hạnh là khi tổng của mori (một ngày nằm trong phân đoạn 1/360 của một năm nhiệt đới) và mieri tăng lên tới 30 thì sẽ tạo ra một tháng nhuận. Cách suy nghĩ này tương tự như một mô tả nào đó trong các tác phẩm kinh điển của Ấn-độ, chẳng hạn như Artha-śāstra. Một mô tả tương tự cũng được tìm thấy trong phiên bản tiếng Trung của văn bản Phật giáo “Lập Thế A-Tỳ-Đàm-Luận” (立世阿毘曇論),[21] được ngài Chân Đế (真諦) dịch vào giữa thế kỷ thứ VI STL.

Thiết nghĩ rằng, đại sư Nhất Hạnh đã biết đến phương pháp Ấn-độ này, và đã thay đổi ý nghĩa của mieri để làm cho nó có ý nghĩa trong bối cảnh lịch Ấn-độ.

II. Đóng góp về toán học của Đại sư Nhất Hạnh: Phát triển phép nội suy

1. Phép nội suy của Đại sư Nhất Hạnh

Nội suy là một phương pháp để ước tính giá trị của hàm f(x) từ các giá trị rời rạc của nó. Ví dụ: f(0), f(1), f(2), v.v… Vì mục đích này, các khác biệt, ví dụ: “khác biệt bậc một” chẳng hạn như Δ­­1 = f(1) – f(0), Δ2 = f(2) – f(1) v.v… và “khác biệt bậc hai” chẳng hạn như Δ2 1 = Δ2 – Δ1, v.v… được sử dụng.

Phép nội suy bậc hai được thiết lập vào thời nhà Tùy bắt nguồn từ phép nội suy bậc một áp dụng cho sai phân bậc một. Vào thời nhà Đường, ngài Nhất Hạnh bắt đầu sử dụng sai phân bậc ba, nhưng phương pháp của ngài không phải là phép nội suy bậc ba.

Đại sư Nhất Hạnh đã áp dụng phép nội suy bậc một cho sai phân bậc hai; nói cách khác, áp dụng phép nội suy bậc hai cho sai phân bậc một, và độ chính xác của kết quả không quá khác biệt so với phép nội suy bậc hai trước đó. Phương pháp của ngài Nhất Hạnh là sự phát triển tự nhiên của phương pháp được sử dụng trong thời Tùy.

Vào thập niên 80 của thế kỷ XX, một số nhà nghiên cứu trẻ Trung Quốc đã nghiên cứu toán học thiên văn Trung Quốc bao gồm cả phép nội suy.[22] Trong số đó, Khúc An Kinh (曲安京) đã xuất bản một chuyên khảo chi tiết về toán học thiên văn Trung Quốc.[23]

2. Phép nội suy ở Trung Quốc trước thời ngài Nhất Hạnh

Những ghi chép sớm nhất về phép nội suy bậc hai ở Trung Quốc được tìm thấy trong lịch Hoàng Cực (皇極暦, năm 600 STL) vào thời nhà Tùy, và một phương pháp tương tự cũng được sử dụng trong lịch Lân Đức (麟徳暦), được sử dụng chính thức từ năm 665 STL trong thời nhà Đường.

Vào đời nhà Thanh (1636-1912), Lý Thiện Lan (李善蘭, 1811-1882) đã giải thích phép nội suy này bằng cách sử dụng mô hình hình học trong Lân Đức Thuật Giải (麟徳術解, năm 1848) của ông. Tuy nhiên, có thể nói rằng, phép nội suy này bắt nguồn từ một phương pháp số học.[24]

Trong phép tính thực tế của phép nội suy này, Δ trong bảng lịch là một cấp số cộng (Δ là hằng số). Do đó, phép nội suy bậc hai có thể được coi là hoàn hảo.

Khi cho Δ1, Δ2, v.v… thu được các giá trị sau:

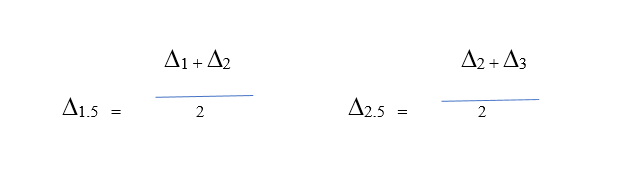
Vì Δ là một cấp số cộng nên phép tính này là chính xác. Từ những giá trị này, giá trị Δ của mỗi ngày (hoặc mỗi độ) có thể được tính toán và tổng của chúng trong một khoảng thời gian nhất định có thể được coi là δ (delta). Ví dụ: giá trị của Δ của một ngày đối với ngày thứ (α + 1) trong khoảng thời gian n ngày (từ Δ1.5 đến  Δ2.5) được coi là: Δ1.5 /n + α (Δ2.5 /n –Δ1.5/n)/n; và ở đây (Δ2.5 /n –  Δ1.5 /n) = (Δ3 /n – Δ2 /n)…

Trên thực tế, phương pháp này có một lỗi nửa ngày, và số nhân của số hạng thứ hai phải là {α + (1/2)} thay vì α. Lỗi này có thể gọi là “vấn đề nửa ngày.” Sau này ngài Nhất Hạnh đã sửa lỗi này.

Để tính f (n + α) từ f(n), f(2n) v.v… thu được giá trị của δ, cho f(n + α) = f(n) + δ. Giá trị của δ có thể thu được bằng cách áp dụng phép nội suy tuyến tính Δ1.5, Δ2.5, v.v… như trên và được áp dụng cho f(n). Đây là phương pháp nội suy bậc hai của f.

Ngài Nhất Hành đã bắt đầu một phương pháp nội suy mới trong đó Δ không phải là một cấp số cộng. Trong trường hợp này, Δ1.5, Δ2.5, v.v... không thể thu được chính xác bằng phép nội suy tuyến tính (do đó ngài Nhất Hạnh đã sử dụng sai phân thứ ba). Sau khi thu được Δ1.5, Δ2.5,  v.v... ngài nhất hạnh đã sử dụng một phương pháp tương tự như phương pháp trước đó để tính f.

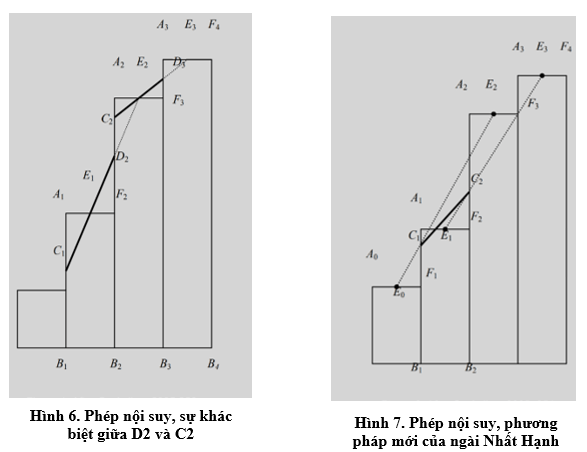
Trong phương pháp thời nhà Tùy, khác biệt đầu tiên là cấp số cộng, nhưng không nằm ở phép nội suy của ngài Nhất Hạnh đã chỉ ra rằng dường như có sự gián đoạn (sự khác biệt giữa D2 và C2, hình 6) nếu phương pháp cũ được áp dụng cho sự tiến triển của ngài Nhất Hạnh và ngài bắt đầu phương pháp mới của mình (hình 7).

Thay lời kết

Đại sư Nhất Hạnh là một nhân vật vĩ đại trong lĩnh vực thiên văn học cũng như Phật giáo, đặc biệt là Kim Cương thừa. Ngài đã đóng góp vào sự phát triển của thiên văn học lý thuyết, thiên văn học quan sát và toán học, cũng như lịch Dayan (大衍暦) là kết quả từ nghiên cứu thiên văn học của ngài, và có thể được  ảnh hưởng một phần nhỏ bởi thiên văn học Ấn-độ. Đây là một chủ đề thú vị và giống như phương pháp nội suy của ngài Nhất Hạnh, cũng cần được nghiên cứu thêm.

Tác giả: Thích Nguyên Định ***

Tài liệu tham khảo

I- Ngoại ngữ

1. Ôhashi, Yukio, 1999a. Historical Significance of Mathematical Astronomy in Later-Han China. In Kim Yung Sik and Francesca Bray (eds.). Current Perspectives in the History of Science in East Asia, Seoul, Seoul National University Press.

2. Ôhashi, Yukio, 1999b. Preliminary remarks on the origin of “Mori” and “Mieri” in Chinese calendars. In Proceedings of the Fourth International Symposium on the History of Mathematics and Mathematical Education using Chinese Characters. Maebashi, Maebashi Institute of Technology.

3. Zhou, L, “The Śārdūlakarṇāvadāna From Central Asia – Introduction.” In Karashima, S. and Vorobyova-Desyatovskaya, M.I. (eds), The St. Petersburg Sanskrit Fragments: Buddhist Manuscripts From Central Asia, Vol. 1. Tokyo: International Research Institute for Advanced Buddhology Soka University, 2015.

4. Linton, C. M., From Eudoxus to Einstein: a history of mathematical astronomy, Cambridge University Press, 2004.

5. Christopher B. F. (ed.), Astronomy before the Telescope, London: The British Museum Press, 1999.

6. Qu Anjing (曲安京), 1997. Dayan-li guiying chafen-biao-de chonggou (《大衍历》晷影差分表的重构) (Reconstruction of a difference table of solar shadow in the Dayan calendar (AD 724). Ziran Kexueshi Yanjiu (Studies in the History of the Natural Sciences), 16, 233-244 (in Chinese). (A Japanese version, translated by Yukio Ôhashi, is in Sūgakushi Kenkyū (Journal of the History of Mathematics, Japan), No.153, 18-29 (1997).)

7. Ôhashi, Yukio, 2000. Mori Mieri qiyuan-kao (没日灭日起源考) (On the origin of Mori and Mieri). Ziran Kexueshi Yanjiu (Studies in the History of Natural Sciences), 19, 264-270 (in Chinese).

8. Yukio Ohashi (Editor: H Selin), Encyclopaedia of the History of Science, Technology, and Medicine. Springer, 1997.

9. Qu Anjing, Ji Zhigang, and Wang Rongbin (曲安京、纪志刚、王荣彬), 1994. Zhongguo gudai shuli tianwenxue tanxi (中国数理古代天文学探析) (Researches on Mathematical Astronomy in Ancient China). Xi’an, Xibei-daxue-chubanshe (in Chinese).

10. Qu Anjing, 2005. Zhongguo lifa yu shuxue (中国历法与数学)(The Chinese Calendar and Mathematics). Beijing, Kexue-chubanshe (in Chinese).

11. Ôhashi, Yukio, 1994b. Zui-Tō jidai no hokan-hō no sanjutsu-teki kigen (隋唐時代の補間法の算術的起源) (Arithmetical origin of Chinese interpolation of the Sui and Tang Periods). Kagakusi Kenkyu (Journal of History of Science, Japan), Series II, 33 (No.189), 15-24 (in Japanese).

II- Hán ngữ

12. [經文資訊]大正藏第 18 冊 No. 0895b 蘇婆呼童子請問經.

13. [經文資訊]大正藏第 18 冊 No. 0893c 蘇悉地羯羅經.

14. [經文資訊]大正藏第 18 冊 No. 0866 金剛頂瑜伽中略出念誦經

15. [典籍資訊]大正新脩大藏經第 32 冊 No. 1644《佛說立世阿毘曇論》.

16. 李淳風 (作 者), 乙巳占, 商務印書館 出版, 1936.

Chú thích:

[1] [經文資訊]大正藏第 18 冊 No. 0895b 蘇婆呼童子請問經.

[2] [經文資訊]大正藏第 18 冊 No. 0893c 蘇悉地羯羅經.

[3] [經文資訊]大正藏第 18 冊 No. 0866 金剛頂瑜伽中略出念誦經.

[4] Đại Nhật kinh sớ là bản sớ giải về kinh Đại Nhật, được ngài Nhất Hạnh viết vào thời nhà Đường, dựa trên sự giải thích của ngài Thiện Vô Úy và có tham khảo nhiều tác phẩm kinh điển. Nội dung của bản sớ giải chủ yếu bao gồm giải thích và thảo luận về âm thanh, ý nghĩa, phân loại, chức năng và phương pháp tu tập.

Còn có các tên gọi khác: Đại nhật kinh bổn sớ (大日经本疏), Đại nhật kinh đại sớ (大日经大疏), Đại nhật kinh vô úy sớ (大日经无畏疏)... Bản kinh sớ này tích hợp Phật giáo Ấn-độ cổ đại và văn hóa Trung Quốc, cũng như hệ thống lý luận của Phật giáo Mật tông thời nhà Đường đều dựa trên kinh sớ này.

[5] Tuế sai: Tuế là năm, sai là sai lệch.

[6] “Ất Tỵ Chiêm” là một cuốn sách chiêm tinh do Lý Thuần Phong viết vào đời nhà Đường, có 10 tập. Xem thêm 李淳風 (作 者), 乙巳占, 商務印書館 出版, 1936.

[7] Xem Ôhashi, Yukio, 1999a. Historical Significance of Mathematical Astronomy in Later-Han China. In Kim Yung Sik and Francesca Bray (eds.). Current Perspectives in the History of Science in East Asia, Seoul, Seoul National University Press, các tr. 259-263; và Ôhashi, Yukio, 1999b.

Preliminary remarks on the origin of “Mori” and “Mieri” in Chinese calendars. In Proceedings of the Fourth International Symposium on the History of Mathematics and Mathematical Education using Chinese Characters. Maebashi, Maebashi Institute of Technology, các tr. 97-102.

[8] Divyāvadāna là một tuyển tập tiếng Phạn gồm các câu chuyện āvadāna của Phật giáo.

[9] Hiện tại Śārdūlakarṇa tồn tại ít nhất ba phiên bản: (1) Một phiên bản ngắn được lưu giữ bằng tiếng Pāli đã trở thành nền tảng cho bản Hán ngữ đầu tiên. Bản dịch (t1300, t551, t552); (2) Phiên bản Trung Á hoàn chỉnh được bảo tồn trong bộ sưu tập St. Petersburg, tạo thành nền tảng của một bản dịch tiếng Trung (T1301) và bản dịch tiếng Tây Tạng; và (3) Bản tiếng Ấn-độ hoàn chỉnh được lưu giữ dưới dạng bản thảo tiếng Nepal.

Trong nghiên cứu Phật giáo, văn bản này nổi tiếng vì nó bao gồm một số quan niệm chiêm tinh sớm nhất của Ấn-độ về các chòm sao trên bầu trời và ứng dụng của chúng trong việc chữa bệnh, quản trị tốt và tích lũy của cải.

Xem thêm Zhou, L,  “The Śārdūlakarṇāvadāna From Central Asia – Introduction.” In Karashima, S. and Vorobyova-Desyatovskaya, M.I. (eds), The St. Petersburg Sanskrit Fragments: Buddhist Manuscripts From Central Asia, Vol. 1. Tokyo: International Research Institute for Advanced Buddhology Soka University, 2015, các tr. 1-5.

[10] Cửu chấp lịch (九執曆), có nghĩa là lịch của ‘chín ngôi sao’, cụ thể là mặt trời, mặt trăng, năm hành tinh và hai ngôi sao tưởng tượng, la hầu (羅睺) và kế đô (計都). Cửu chấp là bản dịch Phạn ngữ Navagraha (có nghĩa là chín ngôi sao). Nó được đặc trưng bởi các phép tính sử dụng các số Ấn-độ, bao gồm số 0 và bởi sự hiện diện của các bảng hàm sin, thay vì số học.

[11]  Hipparchus là một nhà thiên văn học , nhà địa lý học và nhà toán học người Hy Lạp . Ông được coi là người sáng lập ra lượng giác, nhưng nổi tiếng nhất vì khám phá tình cờ của ông về tuế sai của điểm phân. Xem Linton, C. M., From Eudoxus to Einstein: a history of mathematical astronomy, Cambridge University Press, 2004, tr. 52; Christopher B. F. (ed.), Astronomy before the Telescope, London: The British Museum Press, 1999, tr. 81.

[12] Dương Vĩ là một quan chức của Tào Ngụy thời Tam Quốc.

[13] Thị sai trong thiên văn học là góc giữa hai hướng đi qua hai vị trí khác nhau đến thiên thể được quan sát. Khoảng cách của các vật thể trong vũ trụ và cả trên bề mặt trái đất được tính toán bằng cách xác định thị sai, vì thế thị sai trong thiên văn học thường được hiểu là khoảng cách.

[14] Một “độ Trung Quốc” là khoảng cách góc trên thiên cầu mà qua đó mặt trời trung bình

di chuyển trong một ngày.

[15] Xem Qu Anjing (曲安京), 1997. Dayan-li guiying chafen-biao-de chonggou (《大衍历》晷影差分表的重构) (Reconstruction of a difference table of solar shadow in the Dayan calendar (AD 724). Ziran Kexueshi Yanjiu (Studies in the History of the Natural Sciences), 16, 233-244 (in Chinese). (A Japanese version, translated by Yukio Ôhashi, is in Sūgakushi Kenkyū (Journal of the History of Mathematics, Japan), No.153, 18-29 (1997).)

[16] Xích kinh hay xích kinh độ (viết tắt theo tiếng Anh là RA, chữ đầy đủ là Right Ascension; còn được ký hiệu bằng tiếng Hy Lạp α) là một thuật ngữ thiên văn học chỉ một trong hai tọa độ của một điểm trên thiên cầu khi sử dụng hệ tọa độ xích đạo. Tọa độ còn lại gọi là xích vĩ.

[17] Xem Ôhashi, Yukio, 2000. Mori Mieri qiyuan-kao (没日灭日起源考) (On the origin of  Mori and Mieri). Ziran Kexueshi Yanjiu (Studies in the History of Natural Sciences), 19, 264-270 (in Chinese).

[18] Artha-śāstra là từ tiếng Phạn (Sanskrit), có thể được dịch là “khoa học chính trị” hay “khoa học kinh tế” hoặc đơn giản là “nghệ thuật quản lý nhà nước”.

[19] Tithi là thời gian mặt trăng tăng khoảng cách với mặt trời thêm 12 độ. Nói một cách đơn giản, tithi là một ngày âm lịch và lịch tithi đề cập đến âm lịch của đạo Hindu.

[20] Vedāṅga là sáu môn học (1- Shiksha: ngữ âm , âm vị học; 2- Chandas: thi pháp; 3- Vyakarana: ngữ pháp và phân tích ngôn ngữ; 4- Nirukta: từ nguyên, giải thích các từ; 5- Kalpa: hướng dẫn nghi lễ và 6- Jyotisha: chiêm tinh học, thời điểm thích hợp cho các nghi lễ với sự trợ giúp của dấu sao và thiên văn học) phụ trợ của Ấn-độ giáo được phát triển từ thời cổ đại và có liên quan đến việc nghiên cứu kinh Vệ Đà.

Xem thêm Yukio Ohashi (Editor: H Selin),  Encyclopaedia of the History of Science, Technology, and Medicine. Springer, 1997, các tr. 83-86.

[21] Xem [典籍資訊]大正新脩大藏經第 32 冊 No. 1644《佛說立世阿毘曇論》.

[22] Xem Qu Anjing, Ji Zhigang, and Wang Rongbin (曲安京、纪志刚、王荣彬), 1994. Zhongguo gudai shuli tianwenxue tanxi (中国数理古代天文学探析) (Researches on Mathematical Astronomy in Ancient China). Xi’an, Xibei-daxue-chubanshe (in Chinese).

[23] Xem Qu Anjing, 2005. Zhongguo lifa yu shuxue (中国历法与数学)(The Chinese Calendar and Mathematics). Beijing, Kexue-chubanshe (in Chinese).

[24] Xem Ôhashi, Yukio, 1994b. Zui-Tō jidai no hokan-hō no sanjutsu-teki kigen (隋唐時代の補間法の算術的起源) (Arithmetical origin of Chinese interpolation of the Sui and Tang Periods). Kagakusi Kenkyu (Journal of History of Science, Japan), Series II, 33 (No.189), 15-24 (in Japanese).